R、L、C串联和并联的正弦稳态电路

RLC串联的交流电路

下图所示式$R$、$L$、$C$（电阻、电感、电容）三个元件串联的交流电路。电流、电压的参考方向已经标注在图中。

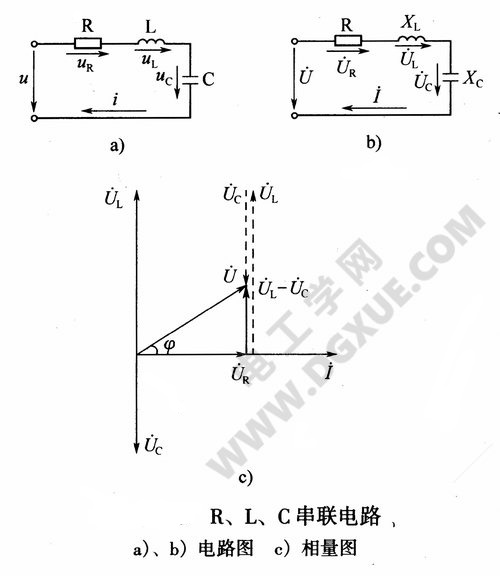
因串联电路中各元件流过同一电路，所以以电流作为参考量。设电流为$i=I_{m}sin\omega t $，则$R$、$L$、$C$各元件上的电压为：

$$ u_{R}=I\sqrt{2}sin\omega t $$

$$ u_{L}=I\sqrt{2}sin\left ( \omega t+90^{\circ} \right ) $$

$$ u_{C}=I\sqrt{2}sin\left ( \omega t-90^{\circ} \right ) $$

根据基尔霍夫定律可知，电路总电压与各元件上的电压代数和相等，即：

$$ u=u_{R}+u_{L}+u_{C} $$

显然，上式中的总电压u是与电流和各元件上电压频率相同的正弦量，可用下式表示：

$$ u=U\sqrt{2}sin\left ( \omega t+\varphi \right ) $$

在上式中只要求出总电压的有效值U和初相位角$\varphi$，则总电压和各元件的电压关系便可知。在此采用相量法分析更为方便。

首先将上图a画成用相量表示的电路图，如图b所示。图中各元件用相应的电阻、电抗、容抗表示，电流、电压用相量表示，则有：

$$ \dot{U}=\dot{U}_{R}+\dot{U}_{L}+\dot{U}_{C} $$

并以$ \dot{I} $为参考相量，做电路的相量图，如图C所示。图中三个元件电压对电流的相位关系分别是$ \dot{U}_{R} $与$ \dot{I} $同相，$ \dot{U}_{L} $超前$ \dot{I} $为90°，$ \dot{U}_{C} $则滞后$ \dot{I} $为90°。将三个元件的电压相量合成，便得到总电压相量$ \dot{U} $。

从相量图中可以得出，总电压有效值为：

$$ U=\sqrt{U_{R}^{2}+\left ( U_{L}-U_{C} \right )^{2}}=I\sqrt{R^{2}+\left ( X_{L}-X_{C} \right )^{2}} $$

相位上，总电压超前电流为$\varphi$角，记为$\varphi$＞0（按习惯规定，电压超前电流时$\varphi$角为正，滞后时为负）。并有：

$$ \varphi =arctan\frac{U_{L}-U_{C}}{U_{R}}=arctan\frac{I\left ( X_{L}-X_{C} \right )}{IR}=arctan=\frac{X_{L}-X_{C}}{R} $$

由上式可知，$\varphi$角是由电路的参数$R$、$X_{L}$和$X_{C}$决定的，如果电路的参数不同，$\varphi$角便不同。若$X_{L}$=$X_{C}$，则$\varphi$=0，电压$\dot{U}$与电流$\dot{I}$相同，此时的电路可看作是电阻性电路；若$X_{L}$＞$X_{C}$，则$\varphi$＞0，电压$\dot{U}$超前$\dot{I}$为$\varphi$角，此时的电路可看作是电感性电路；若$X_{L}$＜$X_{C}$，则$\varphi$＜0，电压$\dot{U}$滞后电路$\dot{I}$为$\varphi$角，此时的电路可看作是电容性电路。

将图C中总电压与分电压关系用下式表示：

$$ \dot{U}=R\dot{I}+jX_{C}\dot{I}=\dot{I}\left [ R+j\left ( X_{L}-X_{C} \right ) \right ]=\dot{I}\left ( R+jX \right )=\dot{I}Z $$

上式称为欧姆定律的相量形式。式中的Z称为复阻抗，单位为Ω。式中X叫做电抗。将上式变换后，得：

$$Z=\frac{\dot{U}}{\dot{I}}=\frac{U\angle \psi _{u}}{I\angle \psi _{i}}=\frac{U}{I}\angle \psi _{u}-\psi _{i}=\left | Z\right |\angle \varphi $$

要注意的是Z只是个复数，它不是时间的正弦函数，即不能用相量表示，故符号Z顶上不能加点。上式中复阻抗的模$\left | Z \right |$称为阻抗，总是正值，即$\left | Z \right |$＞0，单位Ω。$\left | Z \right |$与$R$、$X_{L}$、$X_{C}$有如下关系：

$$ \left | Z \right |=\sqrt{R^{2}+\left ( X_{L}+X_{C} \right )^{2}}=\sqrt{R^{2}+X^{2}}$$

复阻抗$Z$的幅角$φ$叫做阻抗角：

$$\varphi =arctan\frac{X_{L}-X_{C}}{R}=arctan\frac{X}{R}$$

复阻抗可以用复数的各种形式来表示，常用的有：

$$Z=\left | Z \right |\angle \varphi =R+jX=\left | Z \right |e^{j\varphi }$$

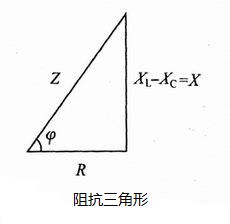在分析计算交流电路时，复阻抗的代数形式和指数形式可按复数的性质进行互换。$R$、$X$和$|Z|$之间又构成了直三角形的关系，称之为阻抗三角形，如右图所示。从阻抗三角形中可知：

$$R=|Z|cosφ$$

$$X=|Z|sinφ$$

练一练

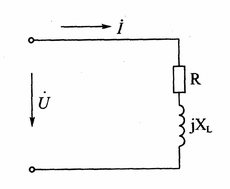题：日光灯电路可用$R$、$L$两个元件串联的电路来表示，如右图所示，其中$R$表示灯管和镇流器的总电阻，$L$表示镇流器的电感，若电阻$R=340Ω$，电感$L$=1.3$H$，正弦电压$U$=220V，求电路中的电流$I$及电阻和电感上的电压。

解：电路总电阻$R$=340$Ω$，镇流器的感抗为：

$$X_{L}=\omega L=2\pi \times 50\times 1.3=480\Omega $$

电路总阻抗为：

$$|Z|=\sqrt{R^{2}+X^{2}}=\sqrt{340^{2}+480^{2}}=532\Omega $$

电流有效值为：

$$I=\frac{U}{|Z|}=\frac{220}{532}=0.414A$$

电阻$R$上的电压为：

$$U_{R}=IR=0.414\times 340=140.76V$$

电感$L$上的电压为：

$$U_{L}=IX_{L}=0.414\times 408=168.91V$$

由计算可知，在$R$、$L$串联的交流电路中，总电压有效值$U$与各元件上电压有效值之和是不相等的，即$U≠U_{R}+U_{L}$。

RLC并联的交流电路

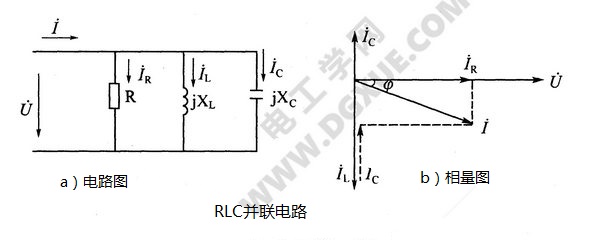
下图是用相量和复阻抗表示的R、L、C并联的交流电路，各电流、电压参考方向已在图中标出。因为各并联支路的电压是相同的，所以取电压作为参考量$u=U_{m}sinωt=U\sqrt{2}sin\omega t$。根据基尔霍夫电流定律，电路的总电流为：$i=i_{R}+i_{L}+i_{C}$。由于并联电路的电源电压和各支路电流时正弦量，所以总电流应为同频率的正弦量。

$$i=I_{m}sin\left ( \omega t+\varphi \right )=I\sqrt{2}sin\left ( \omega t+\varphi \right )$$

由上式可知，只要求出电流的有效值$I$和初相位角$φ$，则i就可以知道了。用相量法作出相量图进行分析。图a中电压、电流用相量表示，各元件参数用电阻$R$、感抗$jX_{L}$和容抗$-jX_{C}$表示，则$i=i_{R}+i_{L}+i_{C}$可写成：

$$\dot{I}=\dot{I}_{R}+\dot{I}_{L}+\dot{I}_{C}$$

以$\dot{U}$为参考量，作电路的相量图，如图b所示。图中三个元件电流对电压的相位关系分别是$\dot{I}_{R}$与$\dot{U}$同相，$\dot{I}_{L}$滞后$\dot{U}$为90°，$\dot{I}_{C}$则超前$\dot{U}$为90°。将三个元件的电流相量合成，便得到总电流相量$\dot{I}$。从相量图中可以得出，总电流有效值为：

$$I=\sqrt{I^{2}_{R}+\left ( I_{L}-I_{C} \right )^{2}}=U\sqrt{\left ( \frac{1}{R} \right )^{2}+\left ( \frac{1}{X_{C}}-\frac{1}{X_{L}} \right )^{2}} $$

相位上，总电流落后电压$φ$角，即为$φ＜0$，并有：

$$\varphi =arctan\frac{\frac{1}{X_{C}}-\frac{1}{X_{L}}}{\frac{1}{R}}$$

由上式可知，$φ$角是由参数$R$、$X_{L}$和$X_{C}$决定的，如果参数不同，$φ$角便不同。若$X_{C}=X_{L}$，则$φ=0$，电压$\dot{U}$与电流$\dot{I}$相同，此时的电路可看作是电阻性电路；若$X_{C}＞X_{L}$，则$φ＜0$，电压$\dot{U}$超前电流$\dot{I}φ$角，此时电路可看作是电感性电路；若$X_{C}＜X_{L}$，则$φ＞0$，电压$\dot{U}$滞后电流$\dot{I}$角，此时的电路可看作是电容性电路。

练一练

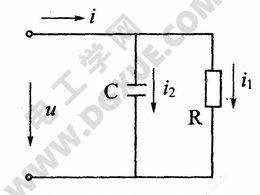题：如右图所示，$R$、$C$并联电路，已知电流有效值$I_{1}=100A$，$I_{2}=100A$，试求总电流$i$的有效值。

解：可用相量法求解。以电压做参考量$\dot{U}=U\angle 0^{\circ}V$，各支路电流相量为：

$$\dot{I}_{1}=\frac{\dot{U}}{R}=\frac{U\angle 0^{\circ}}{R}=I_{1}\angle 0^{\circ}=100\angle 0^{\circ}A$$

$$\dot{I}_{2}=\frac{\dot{U}}{-jX_{C}}=\frac{U\angle 0^{\circ}}{X_{C}\angle -90^{\circ}}=I_{2}\angle 90^{\circ}=100\angle 90^{\circ}A$$

总电流相量为：

$$\dot{I}=\dot{I_{1}+\dot{I_{2}}}=100\angle 0^{\circ}+100\angle 90^{\circ}=100\sqrt{2}\angle 45^{\circ}A$$

总电流有效值为：

$$I=100\sqrt{2}=141.4A$$

其实该题可根据图b和前面的公式直接求出总电流有效值为：

$$I=\sqrt{I^{2}_{R}+I^{2}_{C}}=\sqrt{100^{2}+100^{2}}=100\sqrt{2}=141.4A$$