磁路基本定律：全电流定律、欧姆定律、基尔霍夫定律

对于右图所示的无分支磁路，根据磁通的连续性原理可知，通过铁心各处的磁通Φ相同。

全电流定律

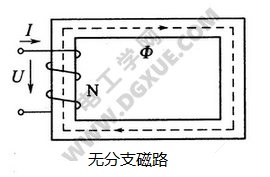对于均匀磁路，即各段磁路的材料以及截面积都相同，全电流定律表示为：

$$Hl=IN$$

上述公式中，l：磁路中心线长度（m），I：线圈电流（A），N：线圈匝数。

对于不均匀的磁路，即各段磁路的材料或者截面积不相同，并且磁路的励磁由若干个线圈通入不同电流共同作用时，全电流定律表示为：

$$\sum Hl=\sum IN$$

公式中$\sum Hl=H_{1}l_{1}+H_{2}l_{2}+\cdots $

$\sum IN=\pm I_{1}N_{1}\pm I_{2}N_{2}\pm \cdots $，各线圈的电流方向与磁场方向符合右螺旋定则时，电流取正号，反之取负号。

练一练

假设上图中的磁路均匀，平均长度l为65cm，线圈匝数N为100，要求铁心的磁感应强度B为0.8T，请分别计算用铸铁、铸钢或硅钢片作为铁心时，线圈应通入多少电流？

解：通过前文《磁的基本知识：磁场、磁路、磁性材料》中的磁化曲线由B=0.8T查出三种材料所对应的磁场强度H，再按照Hl=IN公式计算电流I的数值。

铸铁：B=0.8T是，H₁=26A/cm，所以：

I₁=H₁l/N=26×65/100=16.9A

铸钢：B=0.8T是，H₂=4.5A/cm，所以：

I₂=H₂l/H=4.5×65/100=2.92A

硅钢片：B=0.8T时，H₃=1.2A/cm，所以：

I₃=H₃l/N=1.2×65/100=0.78A

由计算可知，要得到相同的次磁感应强度，采用导磁率更高的硅钢片材料可使线圈电流大大降低，所以电气设备常用硅钢片做成铁心，以减少励磁电流。

磁路欧姆定律

把式H=B/μ代入式Hl=IN，可得：

$$IN=lB/\mu =l\Phi /A\mu=\Phi l /\mu  A$$

如果令Rm=l/μA，称为磁阻；令F=IN，称为磁动势，则：

$$F=\Phi R_{m}$$

上式的形式与电路中的欧姆定律形式相同，所以称磁路欧姆定律。其中Φ类比于电流I，F类比于电动势E，Rm类比于电阻R。一条导线的电阻R=ρl/A，而一段磁路的磁阻Rm=l/μA，课件电阻率ρ类比于导磁率μ的倒数。

对于不均匀磁路，F=ΦRm可以改写成：

$$F=\sum \Phi R_{m}=\Phi _{1}R_{m1}+\Phi _{2}R_{m2}+\cdots +\Phi _{0}R_{m0}$$

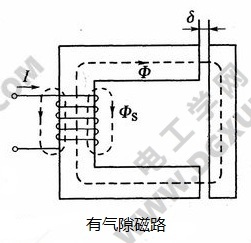对于右图所示的有气隙的磁路，在近似估值时，可用F≈Φ₀R_m0=B₀δ/μ₀，因气隙中的磁压降Φ₀R_m0比各段铁心的磁压降Φ₁R_m1……大得多，这是由于μ>>μ₀所致。气隙中的磁压降比铁心及衔铁的磁压降大得多。

磁路基尔霍夫定律

磁路基尔霍夫第一定律：根据磁通连续原理，对如上图所示的有分支磁路，在磁路的任何一个节点（立体封闭面）上，磁通的代数和等于零，即：

$$\sum \Phi =0$$

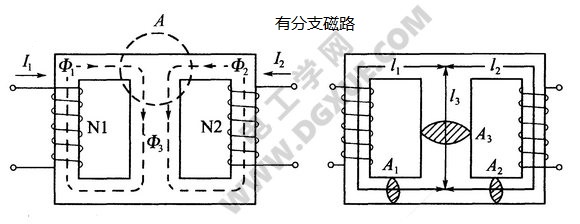
以上图设定的磁通参考方向为正方向，对图中闭合面A，则：Φ₁+Φ₂=Φ₃。

也可以认为，流过节点的磁通代数和等于流出节点的磁通代数和。

磁路基尔霍夫第二定律：与前面的无分支磁路的全电流定律相仿，对有分支磁路存在有：磁路的任一闭合回路中的磁压降Hl的代数和等于该回路的磁动势的代数和，即：

$$\sum  IN=\sum Hl=\sum \Phi R_{m}$$

当回路巡行方向与磁场方向一致时，Hl取正值，反之取负值；当巡行方向与电流方向符合右螺旋定则时，IN取正值，反之取负值。对上图磁路有：

$$\begin{matrix}
I_{1}N_{1}=H_{1}l_{1}+H_{3}l_{3}=\Phi_{1} R_{m1}+\Phi _{3}R_{m3}\\
I_{2}N_{2}=H_{2}l_{2}+H_{3}l_{3}=\Phi_{2} R_{m2}+\Phi _{3}R_{m3}
\end{matrix}$$

通过磁路几个定律的介绍，读者不难发现，磁路定律与电路定律在形式上存在对偶关系。但应特别指出，对偶关系仅是计算形式上相似，而不是说它们的物理性质相同。例如电流是电荷的运动，而磁路中并无磁粒子在移动；电路开路时有电动势存在但无电流，而磁路开路（指有气隙）时，只要磁动势存在就有气隙磁通；电路中电动势为零，电流亦为零，磁路中磁动势为零，但由于有剩磁，故磁通仍不为零；电路中电流通过电阻要损失功率而磁路中，恒定磁通通过磁阻时不消耗能量，即$\Phi ^{2}R_{m}$不表示功耗。就磁路本身来说，维持恒定的磁通并不需要消耗功率，而只有当磁通交变时才会出现功率损耗。

最后需要指出，由于导磁率–的非线性，故磁阻亦是非线性的，用磁路欧姆定律或基氏定律所列出的是非线性方程，在定量计算时是相当困难的。另外，由于电路中的导体与绝缘体的导电率相差几千万倍，故漏电问题不存在。而磁路中磁性材料与空气的导磁率相差仅几千倍，故漏磁往往不容忽略，所以磁路计算的准确度远不及电路计算。

练一练

左右两边对称的磁路如上文中图所示，尺寸为A1=A2=8cm²，$l_{1}=l_{2}=30cm$，A3=20cm²，$l_{3}=10cm$磁性材料是硅钢片。磁动势$I_{1}N_{1}=I_{2}N_{2}$，线圈绕向、电流方向和磁通方向均已标示图上。若要求$\Phi _{3}=0.002Wb$，求两个磁动势各是多少？

解：本题的磁路基氏方程已于正文列过，由于磁路完全对称，故$\Phi _{1}=\Phi _{2}=\Phi_{3}/2=0.001Wb$，则：

$$\begin{matrix}
B_{1}=\Phi_{1}/A_{1}=0.001/(8\times 10^{-4})=1.25T\\
B_{3}=\Phi_{3}/A_{3}=0.002/(20\times 10^{-4})=1T
\end{matrix}$$

根据前文《磁的基本知识：磁场、磁路、磁性材料》查询B—H曲线得知H1=7A/cm，H3=3A/cm，所以：

$$\begin{align}I_{1}N_{1} & =I_{2}N_{2}=H_{1}l_{1}+H_{3}l_{3}\\ & =7\times 30+3\times 10\\ & =240\end{align}$$

240安匝。本题已知Φ求IN则不难，如果已知IN求Φ，则由于非线性，便存在很大困难。